AP Part 4 Quiz
AP Part 4 Quiz awaits! Did you know that the concept of arithmetic progression has roots in ancient times? One of the most famous examples of an arithmetic progression problem comes from the German mathematician Carl Friedrich Gauss. As a child, he was asked to find the sum of all integers from 1 to 100. To the teacher’s surprise, Gauss came up with the correct answer in just a few seconds! He realized that by pairing the first and last numbers (1+100), the second and second-to-last numbers (2+99), and so on, each pair would sum to 101. This simple trick provides a powerful way to solve a variety of AP sums. This AP practice MCQ set tests your understanding of such fundamental concepts.
Sample Questions from This Quiz
- If the numbers (n – 2), (4n – 1) and (5n + 2) are in AP then find the value of n.
- The sum of 3 numbers in AP is 3 and their product is -35. What is the common difference of the AP? [Consider only the positive value]
- The sum of the three numbers in AP is 30 and the ratio of first number to the third number is 3 : 7. Find the common difference.
- The sum of the first three terms of an AP is 33. If the product of the first and the third term exceeds the second term by 29 then find the common difference.
- If the sum of first 14 terms of an AP is 1050 and its first term is 10, find the 20th term.
More Fun Beyond The AP Part 4 Quiz

AP Part 5
Numbers don’t lie, but they sure love confusing you!
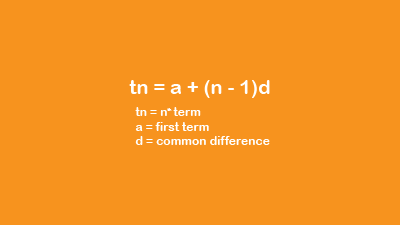
AP Part 2
When numbers line up, fun sneaks in!
AP Part 3
When terms grow up, they still follow the rules!
Trigonometry Part 3
If triangles could talk, they’d totally ace this quiz!

Trigonometry Part 4
The only place where sin, cos, tan are totally legal!

Set Theory Part 1
Sets aren’t for sofas. Test your math brain instead!

Set Theory Part 2
This quiz has more sets than a gym class!

Set Theory Part 3
Sets, subsets, and a dash of chaos await inside!


